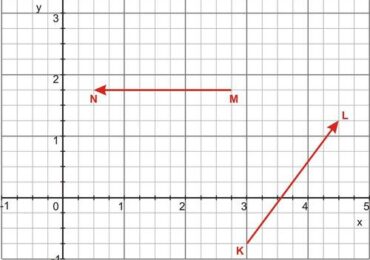
These are two or more lines that are not: intersecting, parallel, or coplanar relative to each other.
For us to comprehend what skew lines are, we need to evaluate the definitions of the following terms:
Parallel Lines are lines that stay on the same plane but never meet.
Intersecting Lines– these lines lie on the same plane and meet.
Coplanar Lines– these are lines that lie on the very same plane.
For instance, if we have lines that do not satisfy these definitions? This is why we need to learn more about skew lines.
In this write-up, you will undoubtedly discover what skew lines are, how to locate skew lines, and identify whether two given lines are skewed.
These lines are a pair of lines that do not intersect or are not parallel to each other. Skew lines can only exist in measurements higher than 2D space. They have to be non-coplanar significance that such lines exist in various planes. In two-dimensional space, two lines can either intersect or parallel each other. Hence, skew lines can never exist in 2D space.
Skew lines can be located in many real-life circumstances. Suppose a line on the ceiling and a line on a wall. If these lines are not parallel to every other and do not intersect after that, they can be skew lines as they hinge on various planes. These lines proceed in two instructions. This short article will discover more about skew lines, their use cases, and how to locate the shortest range between them.
Read Also: Interval Notation – Brief Overview on Working Methodology
The lines and also are instances of two skew lines for every figure. You can know today by seeing exactly how they push different surface areas and are positioned to ensure they are not parallel or intersecting.
What are real-world examples of skew lines?
Because skew lines are located in 3 or more dimensions, our world will undoubtedly have skew lines. Right here are some instances to help you better envision skew lines:
You discovered the lines on the walls and the ceiling’s respective surface areas.
Because the lines on each of the surfaces remain in different planes, the lines within each will never meet, nor will they be parallel.
Two or even more road indications lie along with the same article.
The lines in each road sign are not in the same plane and neither intersect nor parallel to each other.
Roads along freeways and overpasses in a city.
Given that the roads are thought about as separate planes, lines found in each will never ever intersect nor are parallel.
How to find skew lines?
When provided with several real-world instances to discover a set of skew lines, always go back to the meaning. Ask the adhering questions:
What are the lines that do not intersect each other?
Are the selected lines located on a different plane?
Are the picket lines not parallel to every other?
If the solution to the three questions is YES, you have found a pair of 2 lines.
Skew Lines Example
In the real world, we can have various kinds of roads, such as freeways and overpasses in a city. These roads are taken into consideration to be in multiple planes. On such roads, lines drawn will never intersect and are not parallel to every other hence, developing skew lines.
Skew Lines in 3D
Skew lines will remain constantly accessible in 3D space as these lines are always non-coplanar. Intend we have a three-dimensional solid form as shown in examples. We draw one line on the triangle and name it ‘a. We also attract one line on the quadrilateral-shaped face and call it ‘b’. Both an and also b are contained in different planes. If we expand ‘a’ and ‘b’ infinitely in both instructions, they will never intersect, as they are not parallel to every other. Hence, ‘a’ and ‘b’ are examples of skew lines in 3D. In 3D space, if there is a slight deviation in intersecting or parallel lines, it will likely cause skew lines.
Skew Lines Formula
There are no skew lines in the two-dimensional room. In 3 measurements, we have formulas to find the quickest distance between skew lines using the vector and cartesian techniques. To figure out the angle between two skew lines. However, the approach is a bit complicated as these lines never intersect and are not parallel.
Angle In Between 2 Skew Lines
Let’s assume we have two skew lines, PQ and RS. Take a factor O on RS and draw a line parallel to PQ called OT from this point. The angle SOT will give the step of the angle between the two skew lines.
Distance Between Skew Lines Formula
To discover the distance between the two skew lines, you need to draw a line perpendicular to these two lines. We can stand for these lines in the cartesian and vector type to get various kinds of the formula for the fastest distance between two picked skew lines.
In the state, we have two skew lines, P1 and P2. In the following section, we will study the methods to locate the distance between two skew lines.