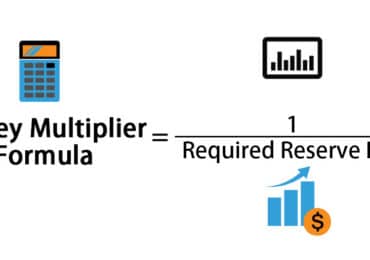
There are circumstances where the expression for the functions is based on the provided input value’s interval. When this occurs, we call these types of functions piecewise-defined functions.
We use piecewise functions in our lives more than we assume so. Tax obligation brackets, estimating our mobile phone plans, and even our incomes (with overtime pay) use piecewise functions.
This is why we have allotted a unique short article for this function. In this short article, you’ll discover the following:
Meaning of the piecewise function.
Discovering exactly how to examine piecewise-defined functions at provided intervals.
Graphing and interpreting piecewise functions.
What is a piecewise function?
Recognizing what piecewise functions are and how we can build our piecewise-defined functions allows the initial study and a much deeper understanding of exactly how it works.
Piecewise function meaning
It is a function explained by various formulas or functions for every provided interval. It’s also in the name: piece. Pieces of functions specify the function for every part of the domain.
As seen from the use case shown over, f( x) is a piecewise function since it is determined distinctively for the intervals: x > 0, x = 0, and x < 0.
Strategy to check out piecewise functions.
When we have an offered piecewise-defined function, we can translate it by looking at the provided intervals. If we have a look at our instance, we can review it as follows:
f(x) is equivalent to 1, When x equals 0
f(x) is equivalent to 2x, When x greater than 0
f(x) is equal to -2x, When x less than 0
When given a piecewise function graph, see to it to observe the offered intervals where f( x) has various graphs. Before we experiment with examples that entail examining piecewise function graphs. Let’s go ahead and find out just how we can assess and graph piecewise functions first.
How to resolve piecewise functions?
Since we’ve discovered this unique function, how do we ensure that we return the appropriate value for the function offered x? Here are ideas to remember when solving for as well as evaluating piecewise functions:
Double-check where x hinges on the provided interval.
Review the value-making use of the matching function.
How does the graph piecewise function?
As stated, piecewise functions have various functions for every offered interval. This suggests that when putting piecewise functions in a graph, anticipate different graph functions for every break too.
Right here are some quick tips when graphing piecewise functions:
It assists in determining how each function would appear like.
For inclusive intervals (i.e. x ≥ 0), consisting of the endpoints.
For exclusive intervals (i.e. x < 0), leave out the endpoints by utilizing unfilled dots.
What typical functions may you run into when graphing piecewise functions? Right here are some resources, and also feel free to take a look at the links to freshen your expertise on a few of the commonly used graphs:
Linear functions, for instance, y = 4x, f(x) = 3x -1 and more.
Quadratic functions such as y = -3 x2 + 4x, f(x) = 2×2– 1, and extra.
Cubic functions for instance, f(x) = 4×3 + 1, y = -x3-1, as well as extra.
Piecewise functions cannot use only these functions, so see to it additionally to check your textbook’s collection of functions whenever you require. Let’s graph the piecewise function given in the first section.
f(x) = 1, for x=0
f(x) = 2x, for x>0
-2x, for x<0
When x < 0, f( x) and x > 0 return to a linear function. Discover at the very least two pairs of points that please each function and utilize them to create linear graphs.
We are considering that both are exclusive inequalities. The dot at the origin will leave unfilled. Now, we are entrusted with the condition when x = 0. Given that the value is constant at f( x) = one let’s plot a graph at (0,1).
This returns the final graph for the offered piecewise function. From the graph, we can observe that f( x) has a domain of as well as a series of (- ∞, ∞) and also [0, -∞), specifically.
Read Also: Parent Functions
We’ve covered all the essential residential or commercial properties and methods we can use with functions, so it’s time for us to review our expertise with these examples!
Example
Graph the piecewise function shown listed below. Using the graph, establish its domain and also range.
f(x) = 1, for x equals to 0
f(x) = 2x, for x not equals to 0
Solution
For all intervals of x aside from when it is equivalent to 0, f(x) = 2x (which is a direct function). To put the linear function graph, we can use 2 to indicate the line. See to it that the two points satisfy y = 2x. Ensure to leave the point of origin as it is.
Also, when f(x) = 1 when x = 0, we outline a loaded point at (0,1). The graph over shows the final graph of the piecewise function.
Considering that the graph includes all values of x, the domain would be all actual numbers or (-∞, ∞). The same thinking applies to the series of functions. Considering that it expands in both instructions, the sequence of the function is (-∞, ∞) in interval notation.