Determinant calculator: The component of a matrix is a number calculated from a square matrix. It uses for fixing systems of direct formulas as well as informs us regarding particular residential properties of the matrix, such as the volume scaling variable of the linear change defined by the matrix.
The matrix determinant can likewise aid us if the matrix has an inverted matrix or not. Also, significantly, the determinant assists us in finding the eigenvalues.
How to Calculate a Determinant by Hand
The method for determining the composition of a matrix depends upon the dimension of the matrix. For a one × one matrix, the component is the number inside the matrix. For anything two × two and more significant, we use shortcut methods that have a particular order of increasing, including, and subtracting components.
Understand more about Matrix
One of the simplest, most unique operations you can execute with a matrix is called the factor. In this video, we’re most likely to focus on what it appears like and exactly how you calculate it. We’re not going to go too comprehensive, yet little matrix necessary, and vocabulary required for us to this.
Matrices are grids of numbers surrounded by brackets, a sort of squared-off parentheses as well as matrices are classified by the number of rows and columns. Hence, called a matrix, an M x N matrix, where M is the variety of rows and N is the variety of columns. What you see right here is a 3 x 5 matrix since it has five columns and three rows of numbers, which is a total of 15 numbers inside. This would undoubtedly be a six by 1 (6 x 1) matrix as a result of its six rows and also just 1 column. Both of these instances look like rectangular shapes because the number of rows, as well as columns, are various.
The determinant of a Matrix
A matrix is beneficial when addressing a system of formulas. An example of when a matrix is made use of is when resolving a collection of formulas created from Kirchhoff’s policies when evaluating an electrical circuit having resistors and batteries. Many times, there are unidentified resistor numbers, battery voltages, and also currents in various parts of the channel. A matrix makes solving the three or more equations much less complicated than resolving the equations algebraically. Let’s work with fixing for the component in some matrices.
Working of Determinant Calculator
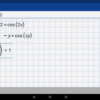
The determinant calculator makes use of the same requirement two × 2 matrix specific technique that a human use. The picture over shows this approach applied to a 3 × 3 matrix.
Considering that the calculator can take care of as much as a 5 × 5 matrix, the software program powering it actually breaks down big matrices into numerous 2 × 2 determinants address sequentially. It is accurate to a minimum of the fifth decimal area!

As soon as the component from the inputted matrix calculated, it is sent back and presented on the webpage.
Matrices and Linear Algebra – Basic Overview
Linear algebra is a significant location of mathematics, with various scientific applications. One of the most fundamental principles in linear algebra is the principle of a matrix. A matrix is a rectangular range of numbers. There is a significant amount related to square matrices, referred to as the determinant, which, if nonzero, indicates that the matrix has a well-defined inverse.
Linear algebra is mainly interested in solving systems of linear formulas. Such a system represented as a matrix formula of the type Ax = b, where A is the matrix of coefficients of the formulas, x is a column vector having all the unknown quantities of the formulas, as well as b is the column vector of consistent terms of the equations. Several techniques for solving such a system of equations, each involving matrix operations. If A is an invertible square matrix, after that, the system has a one-of-a-kind solution of the kind x = A ^ -1 B, where A ^ -1 is the inverse of A.
Final Words
The above formula can continuously use to address a system of n direct formulas in n variables. It is usually impractical to do so directly. There are a lot of more efficient approaches, which do not call for calculating the inverse. The fastest method is Gaussian elimination, which is a form of row decrease. The idea is to do a sequence of linear procedures on the rows of the enhanced matrix [| b], formed by including the column vector b to the ideal side of the matrix A. When the procedure is total. We entrust to the matrix [I|x], where I am the identity matrix, and x is the column vector of services.
Although matrices primarily used for solving systems of straight equations, they have lots of other uses also. An additional application of matrices is in performing direct changes of collaborates. These consist of representations, turnings, stretches as well as shears.
Read Also: Double Integral Calculator – A Complete Overview