What Is Vertex Form? Example

In geometry, a vertex form is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices. For example, a square has four corners, each is called a vertex. The plural form of the vertex is vertices. The word vertex is most commonly used to denote the corners of a polygon.

When two lines meet at a vertex, they form an included angle. For polygons, the included angle at each vertex is an interior angle of the polygon. Vertex is also sometimes used to indicate the ‘top’ or high point of something, such as the vertex of an isosceles triangle, which is the ‘top’ corner opposite its base, but this is not its strict mathematical definition.

Vertex Form Of Equation

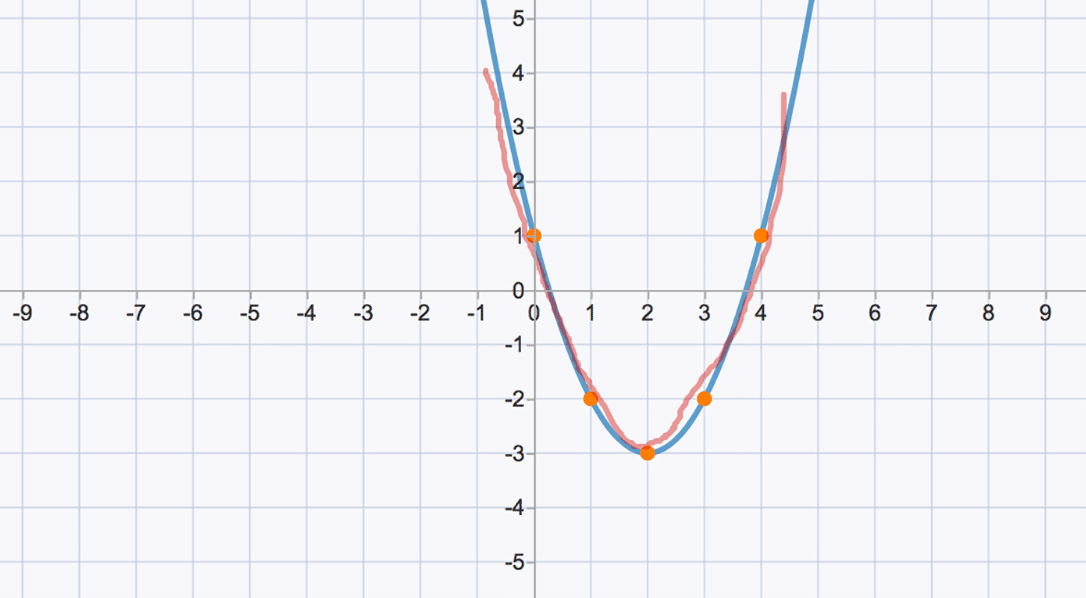
The vertex form of a parabola’s equation is generally expressed as: y = a(x-h)²+k

(h,k) is the vertex as you can see in the picture below
If a is positive then the parabola opens upwards like a regular “U”.
If a is negative, then the graph opens downwards like an upside down “U”.
If |a| < 1, the graph of the parabola widens. This just means that the “U” shape of parabola stretches out sideways . Explore the way that ‘a’ works using our interactive parabola grapher.
If |a| > 1, the graph of the graph becomes narrower(The effect is the opposite of |a| < 1).

Standard Form To Vertex Form

The standard form of a quadratic equation is y = ax^2 + bx + c, where a, b, and c are coefficiencts and y and x are variables. It is easier to solve a quadratic equation when it is in standard form because you compute the solution with a, b, and c. However, if you need to graph a quadratic function, or parabola, the process is streamlined when the equation is in vertex form. The vertex form of a quadratic equation is y = m(x-h)^2 + k with m representing the slope of the line and h and k as any point on the line.

Factor Coefficient

Factor the coefficient a from the first two terms of the standard form equation and place it outside of the parentheses. Factoring standard form quadratic equations involves finding a pair of numbers that add up to b and multiply to ac. For instance, if you are converting 2x^2 – 28x + 10 to vertex form, you first need to write 2(x^2 – 14x) + 10.

Divide Coefficient

Next, divide the coefficient of the x term inside the parentheses by two. Use the square root property to then square that number. Using that square root property method helps to find the quadratic equation solution by taking the square roots of both sides. In the example, the coefficient of the x inside the parentheses is -14.

Balance Equation

Add the number inside the parentheses, and then to balance the equation, multiply it by the factor on the outside of parentheses and subtract this number from the whole quadratic equation. For example, 2(x^2 – 14x) + 10 becomes 2(x^2 – 14x + 49) + 10 – 98, since 49*2 = 98. Simplify the equation by combining the terms at the end. For example, 2(x^2 – 14x + 49) – 88, since 10 – 98 = -88.

Convert Terms

Finally, convert the terms inside parentheses to a squared unit of the form (x – h)^2. The value of h is equal to half the coefficient of the x term. For example, 2(x^2 – 14x + 49) – 88 becomes 2(x – 7)^2 – 88. The quadratic equation is now in vertex form. Graphing the parabola in vertex form requires the use of the symmetric properties of the function by first choosing a left side value and finding the y variable. You can then plot the data points to graph the parabola.

Solved Examples Of Vertex

Question: Find the vertex of the parabola: y=3x2+12x−12

Solution:

Given,
a= 3
b = 12

So, the x-coordinate of the vertex is:

−122(3)
=-2

Substituting in the original equation to get the y-coordinate:

y=3(2¯¯¯)+12(−2)−12
=-24

So, the vertex of the parabola is at (-2, -24).

Vertex Form Of A Quadratic

The vertex form of a quadratic is given by y = a(x – h)² + k, where (h, k) is the vertex. The “a” in the vertex form is the same “a” as in y = ax² + bx + c (that is, both a‘s have exactly the same value). The sign on “a” tells you whether the quadratic opens up or opens down. Think of it this way: A positive “a” draws a smiley, and a negative “a” draws a frowny. (Yes, it’s a silly picture to have in your head, but it makes it very easy to remember how the leading coefficient works.)

In the vertex form of the quadratic, the fact that (h, k) is the vertex makes sense if you think about it for a minute, and it’s because the quantity “x – h” is squared, so its value is always zero or greater; being squared, it can never be negative.

Suppose that “a” is positive, so a(x – h)² is zero or positive, and, whatever x-value you choose, you’re always taking k and adding a(x – h)² to it. That is, the smallest value y can be is just k; otherwise y will equal k plus something positive. When does y equal only k? When x – h, the squared part, is zero; in other words, when x = h. So the lowest value that y can have, y = k, will only happen if x = h. And the lowest point on a positive quadratic is of course the vertex.

If, on the other hand, you suppose that “a” is negative, the exact same reasoning holds, except that you’re always taking k and subtracting the squared part from it, so the highest value y can achieve is y = k at x = h. And the highest point on a negative quadratic is of course the vertex.