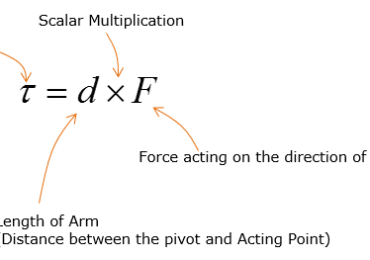
Causal Inference: Causal inference is the process of drawing a conclusion about a causal connection based on the conditions of the occurrence of an effect. The main difference between causal inference and inference of association is that the former analyzes the response of the effect variable when the cause is changed. The science of why things occur is called etiology. Causal inference is an example of causal reasoning.
Causal inference, or the problem of causality in general, has received a lot of attention in recent years. The question is simple, is correlation enough for inference? I am going to state the following, the more informed uninformed person is going to pose a certain argument that looks.
Causal Inference In Statistics
Causal inference refers to an intellectual discipline that considers the assumptions, study designs, and estimation strategies that allow researchers to draw causal conclusions based on data. As detailed below, the term ‘causal conclusion’ used here refers to a conclusion regarding the effect of a causal variable (often referred to as the ‘treatment’ under a broad conception of the word) on some outcome(s) of interest.
The dominant perspective on causal inference in statistics has philosophical underpinnings that rely on consideration of counterfactual states. In particular, it considers the outcomes that could manifest given exposure to each of a set of treatment conditions. Causal effects are defined as comparisons between these ‘potential outcomes.’ For instance, the causal effect of a drug on systolic blood pressure 1 month after the drug regime has begun (vs no exposure to the drug) would be defined as a comparison of systolic blood pressure that would be measured at this time given exposure to the drug with the systolic blood pressure that would be measured at the same point in time in the absence of exposure to the drug.
The challenge for causal inference is that we are not generally able to observe both of these states: at the point in time when we are measuring the outcomes, each individual either has had drug exposure or has not.
Causal Inference In Statistics
Yoshua Bengio, one of the world’s most highly recognized AI experts, explained in a recent Wired interview: “It’s a big thing to integrate [causality] into AI. Current approaches to machine learning assume that the trained AI system will be applied to the same kind of data as the training data. In real life, it is often not the case.”
Yann LeCun, a recent Turing Award winner, shares the same view, tweeting: “Lots of people in ML/DL [deep learning] know that causal inference is an important way to improve generalization.”
Causal inference and machine learning can address one of the biggest problems facing machine learning today — that a lot of real-world data is not generated in the same way as the data that we use to train AI models. This means that machine learning models often aren’t robust enough to handle changes in the input data type, and can’t always generalize well. By contrast, causal inference explicitly overcomes this problem by considering what might have happened when faced with a lack of information. Ultimately, this means we can utilize causal inference to make our ML models more robust and generalizable.
Causal Inference Book
For causal inference, there are several basic building blocks. A unit is a physical object, for example, a person, at a particular point in time. Treatment is an action that can be applied or withheld from that unit. We focus on the case of two treatments, although the extension to more than two treatments is simple in principle but not necessarily so with real data.
Associated with each unit are two potential outcomes: the value of an outcome variable Y (e.g., test score) at a point in time t when the active treatment (e.g., new educational program) is used at an earlier time t0, and the value of Y at time t when the control educational program is used at t0. The objective is to learn about the causal effect of the application of the active treatment relative to the control (treatment) on Y. Formal notation for this meaning of a causal effect first appeared in Neyman (1923) in the context of randomization-based inference in randomized experiments. Let W indicate which treatment the unit received: W = 1 the active treatment, W = 0 the control treatment.
Moreover, let Y(1) be the value of Y if the unit received the active version, and Y(0) the value if the unit received the control version. The causal effect of the active treatment relative to its control version is the comparison of Y(1) and Y(0) – typically the difference, Y(1) – Y(0), or perhaps the difference in logs, log[Y(1)] – log[Y(0)], or some other comparison, possibly the ratio. The fundamental problem for causal inference is that, for any individual unit, we can observe only one of Y(1) or Y(0), as indicated by W; that is, we observe the value of the potential outcome under only one of the possible treatments, namely the treatment actually assigned, and the potential outcome under the other treatment is missing. Thus, inference for causal effects is a missing-data problem – the “other” value is missing. Of importance in educational research, the gain score for a unit, posttest minus pretest, measures a change in time, and so is not a causal effect.