If you’re looking for a way to find the domain of a function, then you’re in the right place! In this article, we’ll take a look at how to calculate the domain of a function on a graph, using a Rational, Absolute value, and Identity function.
Identity function
The identity function is a mathematical function that maps real numbers to itself. It has three properties: it is bijective, it has an inverse and it is invertible. All of these characteristics make it a valuable tool for engineers, scientists and mathematicians.
To explain the identity function, we first need to understand the definition of an identity. Identity is a one-one function, which means that it maps a single element of a set to itself. This can be done in various ways, including through a graph or through a set of functions.
Read Also: What Is Vertex Form? Example
For example, an identity function graph can be written as (x, I(x)) or (x, id(x)). These two forms are both equivalent. A graph is a set of lines that passes through an origin. An identity function is a real-valued function, so the value of every point on the graph corresponds to the same value on the x and y axes.
Absolute value function
When you’re evaluating a real number, you need to know the absolute value function. The absolute value function is a math tool that shows you the difference between the number you’re evaluating and zero. It’s also useful for graphing.
There are three different ways to write an absolute value function. One way is an algebraic approach. The other two are set-builder and interval notation. Regardless of the method you choose, you need to be sure to write the function in the right form.
Normally, an absolute value function has a V-shaped graph. The tip of the V is usually the 0 and the other is the h or k. Depending on the values you use for h and k, the tip will change.
Inset: Absolute value functions can be written in interval, set builder and even root notation. However, a better approach is to use the vertex-based form. This is the best method because it will be easier to read.
An important aspect of the vertex-based form is the point where the function changes direction. Typically, the first step in graphing an absolute value function is to determine the vertex. You can do this by either using your graphing calculator or by hand.
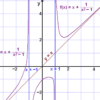
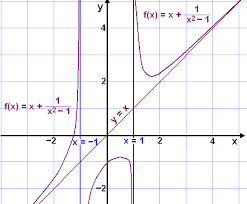
Rational function
The first step in understanding rational functions is to find the domain of the function. The domain is the set of values in the function that are real numbers and are not zero. In addition, this includes any number that is greater than or equal to three.
A rational function is defined by f(x) = p(x) / q(x). In the example, f(x) has three x-intercepts: x = 0 and x = 2. These are the points on the x-axis where the function crosses. It can also have vertical asymptotes. There is one such asymptote at x = 4.
There are a few methods for finding the inverse of a rational function. One of them is graphing. This involves drawing a graph with two columns. However, it can be very tedious at first.
Range of a function
Range of a function is a mathematical concept which is basically a set of all x-values and y-values that a function produces. It’s a set of possible outcomes for the dependent variable. Usually, the range is expressed as an equivalence or less than symbol.
For instance, if f(x) is a straight line, the range is the longest distance from x to y. The range can be defined by a number of different methods.
A function may also be defined by its codomain. This is a subset of the range. Generally, the codomain of a function is also the domain of the function.
The domain of a function is a set of all the values that a function takes as inputs. It’s also the set of all the outputs a function can produce.
Typically, the domain of a function is more difficult to determine from a formula. One way to look for the domain of a function is to examine the graph of the function. This can help to determine the y-values in a function.
Calculating domain on a graph
If you are a student learning to use a graphing calculator, you may want to learn how to calculate domain. Domain is a set of all x and y values that can go into a function. The domain of a function can be found either by looking at the graph or by using a domain and range calculator.
To determine the domain of a graph, you first need to look at the axis and identify the function. Some functions are easier to find than others. For example, the domain of a quadratic function is all of the real numbers on the x-axis. You can easily check the domain of a function by calculating the square root of the function’s denominator.
Once you have a list of x and y coordinates, you can then use a domain and range calculator to discover the range of a function. These calculators will find a list of x-values that will generate y-values.
A domain is a set of all input and output values that can be derived from a given function. In a line graph, this can be described by interval notation.