If you have been given a trigonometric function or a quadratic function, you may be wondering how to find horizontal asymptotes in your work. In fact, there are some methods for doing this.
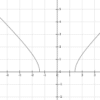
An explanation of horizontal asymptotes on graphs
-
Graphing time on x-axis and concentration on y-axis
When you’re working with a graph, it’s good to know a few tricks of the trade. For example, if you’re drawing a scatter plot, you can use a regression line to get the most accurate picture of the relationship between two variables.
A scatter plot is a type of graph that displays changes in two continuous variables at once. This can be done by using a curve, trendline, or regression line.
The first step is to choose a scale and label the axes. Typically, a scale runs from low to high in easily counted multiples. For example, the scale may run from 0.1 to 10 on the y axis, if you’re drawing a graph of height and weight.
A line graph is the best choice for displaying change over a continuous range. It’s also the easiest to read if your data points are spaced widely apart. However, if your data is very close together, reading a graph can be difficult.
If you’re not ready to take on the task of a full blown graph, try using a scatter plot. These are easier to read because they display changes in two or more different samples at the same time.
In the same vein as a scatter plot, a straight line can be drawn through the data and used to calculate the slope of a line. This is done by extending the line to the extremes of the graph paper and using logarithms to get the correct scale.
-
Graphing trigonometric functions
The asymptotes of a trigonometric function can be found in a number of ways. These asymptotes may be vertical or horizontal. When you find an asymptote on a graph, it can be used to determine its value. You can also find an asymptote by writing a rational function. In addition, some functions have asymptotes that are neither horizontal or vertical.
One method of finding an asymptote is to check the degrees of the numerator and denominator. By checking these degrees, you can find the y-coordinate of the function. Once you have the y-coordinate, you can draw a line that goes from zero to the asymptote.
Asymptotes are a type of function limit. They can be determined by computing the limits of a function. It is important to note that the asymptote is not the same as the point where the function ends. There are many other factors that affect the location of an asymptote.
Horizontal asymptotes are a type of asymptote that are very easy to find. To find the horizontal asymptotes, you can look at the graph of the function. For example, the function y = x/(x-1) will be a horizontal asymptote. This is because the graph of the function jumps from negative infinity to positive infinity.
-
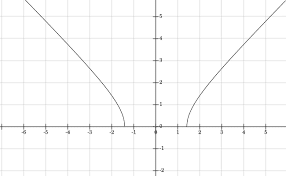
Graphing quadratic functions
When graphing a function, you will need to determine the horizontal asymptotes of the graph. These are imaginary lines that are close to the graph and help you to see curves. For example, the horizontal asymptote of the graph y = f(x) is the equivalent of y = 0 and the vertical asymptote of the graph is y = f(x)+2 (x + 1).
Horizontal asymptotes can be found by dividing the leading coefficients in the function. The method to find horizontal asymptotes varies according to the degree of the polynomials. It starts by cancelling the factors of the denominator and re-dividing the numerator and leading coefficients.
The numerator is usually quadratic. Its degree is one less than the degree of the denominator. If the numerator has a leading term that is larger than the denominator, the function will have an oblique asymptote. On the other hand, if the numerator has a leading term smaller than the denominator, the function has a slant asymptote.
If the function has a quadratic denominator, there will be at most two distinct roots. A quadratic function will also have no vertical asymptotes. You can find all the roots of a quadratic function by factoring the top and the bottom. However, if you want to solve the equations, you can use the square root method. This method will also reveal the corresponding domain and range.
-
Identifying if a horizontal asymptote exists
Horizontal asymptotes are the places where a function approaches infinity. They are horizontal lines that intersect a graph. They describe the end behavior of a function depending on the input value. A function’s asymptotes can have a maximum of two horizontal asymptotes. However, there are functions that have asymptotes that are neither vertical or horizontal. For example, a reciprocal function will have a vertical asymptote. Similarly, a rational function will have a slant asymptote.
In order to find a horizontal asymptote, you first need to determine its location. You can do this by dividing the coefficients of the highest degree terms. For example, if a function has a numerator that is x and a denominator that is b, then the asymptote is located at x = b.
Vertical asymptotes occur at x = p/2, x = 3p/2, and x = -2. This is because the leading coefficients are p(x), q(x) and q(x)+p(x). The coefficients are also written as p(x) and q(x) for f(x)=,q(x)0. As the function approaches infinity, the leading coefficients will increase, and the limit will become y = x/(x-1). Likewise, y = x/(x-1) becomes x/x.