How to Find Average Rate of Change

How to find average rate of change is an important mathematical concept to know. It can be used to estimate changes in your sales applications, or to calculate the average rate of change in a word problem. The process is quite simple, and is a common technique. You just need to know how to perform the calculation.

Method to Calculate a linear function

A linear function is a function which has the same average rate of change over any interval. This is usually expressed as an expression in the form of a slope. The slope can be seen in the graph of a function, the table, or the equation.

An increasing function has a positive rate of change. On the other hand, a decreasing function has a negative rate of change. In both cases, the output is larger than the input. It is important to understand that this is a characteristic of functions. A line can be in either point-slope or slope-intercept form. If the line is in the latter form, then its slope is m.

Linear functions are very easy to calculate. They also perfectly model constant rate changes. These functions are used in many scientific and technical applications. One example of a function is the number of occupied apartments. Another is the cost of gasoline. The price of gas has seen wild fluctuations in the last few decades.

The average rate of change of a function is derived from the slope of a line connecting the endpoints of an interval. To get this rate of change, find the values of a function at each of the endpoints in the interval. Next, subtract the value of the function at the first point from the value of the function at the second point. When the average rate of change is zero, this means that the values of the two points have the same slope.

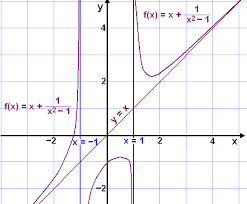
Calculating a non-linear function

When working with nonlinear functions, it is important to understand how to calculate an average rate of change. A rate of change is a formula that divides the change in x-values by the change in y-values. It is often used in order to determine the slope of a graphed function.

For example, if you have data on the number of fish in a pond, you can use the average rate of change equation to calculate how many more fish will be caught in a certain amount of time. An average rate of change is also used to calculate the speed of an object, such as a car.

Calculating an average rate of change is a common concept in calculus. However, the process of calculating an average rate of change can be a bit confusing. The process can be simplified using a concept map. This helps students select the best problem solving strategy. In addition, students can practice less challenging problems before moving onto the more difficult ones.

Depending on the type of function you’re working with, you can find an average rate of change in either equation or graph form. Linear functions are always straight lines, while nonlinear functions have a graph of some sort.

Calculating the average rate of change from a word problem

The average rate of change, or AROC, is a fancy-pants mathematical term for the rate at which one item changes in relation to another. The average rate of change can be calculated in two ways. First, by looking at the rate of change over an interval. This is done by looking at the values of the function at both ends of the interval. Second, by calculating the slope of the line that passes through the two points.

Read Also: What Is Bass Clef Notes?

In general, the average rate of change is the best measure of how one thing changes in relation to another. It can be calculated by taking the average of the values at both ends of an interval and multiplying the result by a scalar. For instance, if the function f(x) at both ends is x2 – 9x, the average rate of change is x2 – 9.5x.

There are other forms of AROC, such as the AROC of a function. For instance, the average rate of change of a function that is increasing may be a negative number, and vice versa. On the other hand, the rate of change of a function that is decreasing may be positive. One way to determine this is by looking at the slope of a straight line that passes through the two points.

Calculating the average rate of change in sales applications

If you are looking for some insight into sales applications, one of the most useful tools that you can use is the average rate of change. This can be calculated using a simple algebraic formula. For example, to calculate the rate of change of g(x) for a function, you need to have a x value and an interval length of 0.2.

In other words, you need to calculate the rate of change for both x and x+2, and then apply the result to both sides of the interval. The average rate of change is a good way to measure the impact of price, margins, and other factors on the sales of a product.

Average rate of change is also a good indicator of how quickly a product changes over time. For example, if a product goes from a tenth to an eighth in cost, you can determine that the rate of change is five percent. You can then use the result to estimate the instantaneous rate of change.